攻防世界一波Crypto的学习

0x01前言

前两天有一个学长喊我给他做几道XCTF平台上的密码题，刚好之前一直很少接触，这次也当作是初学密码了

0x02题目

NTRU sample(GFSJ1205)

tell_aes_app(GFSJ1187)

Uncommon Factors II(GFSJ1149)

Equation(GFSJ1120)

babyECC2(GFSJ1119)

Red Alert 2（速来1v1）(GFSJ1104)

crypto_rsa2(GFSJ1054)

crackme_c(GFSJ0039)

babyrsa(GFSJ0114)

wacky-agent-75(GFSJ0211)

salsa(GFSJ0222)

sleeping-guard(GFSJ0434)

mix(GFSJ0750)

babystream(GFSJ0821)

圆舞曲(GFSJ0824)

#椭圆曲线加密ECC

题目描述：Tover说不想出题了，我把他上年的防AK题改了一下（逃随机数生成器就是逊啦，xor yyds！

华南师范大学的一个新生赛题

先看看附件的代码，并分析了一下代码的意思

#sage
from secret import flag
import random

bits = 64
p = random_prime(2^bits)#生成一个64位的随机素数p
a = randint(1, bits)
b = randint(1, bits)#生成两个随机整数a和b作为椭圆曲线的参数
E = EllipticCurve(GF(p), [a, b])#生成了一个椭圆曲线E，llipticCurve 是 SageMath 中用于定义椭圆曲线的函数。
g = E.random_element()#从曲线上随机取一个点g

x = random_prime(2^16)#生成一个16位的随机数
pk = x*g#生成公钥pk
k = randint(1, p-1)#生成随机数k用于加密算法
kPoint = k*pk
kp = kPoint.xy()#提取 kPoint 的坐标 (x, y)，并将其存储在 kp 中。

c = []#一个空列表
for i in range(len(flag)):#遍历flag的字符
  c.append( (ord(flag[i]) ^^ int(kp[i%2])) & 0xff )
#将字符转化成ASCII码值，并与kp中的坐标值进行异或XOR操作，并将结果限制在 0 到 255 之间后将结果添加到列表 c 中。
c = bytes(c).hex()#将列表 c 转换为字节，并转换为十六进制字符串。

print(p)
print(a)
print(b)
print(g)
#print(g.order())
print(c)


#out
'''
4698491801183562589
58
59
(2965797230620625775 : 4310564666276679314 : 1)
ac73a774a25bd512d543dc468542c9428141800dd041d043c918d112850dd515d6128214d1138211d71599

'''

out文件就是sage文件代码中的五个输出

是基于椭圆曲线加密(ECC)的简单加密算法，加密的内容就是flag

加密过程很简单，就是将flag的第i个字符与kp的两个分量进行异或，但是这里可以注意到

并且这是华师2021年的新生赛，flag格式当时写的是HSCTF{}或者hsctf{}，所以kp还是可以爆出来的

这道题还是很简单的，把kp爆破出来然后解密就行了

c = 'ac73a774a25bd512d543dc468542c9428141800dd041d043c918d112850dd515d6128214d1138211d71599'
c = bytes.fromhex(c)
#print(c)
#flag:HSCTF{...}
key = [c[0]^ord('H'),c[1]^ord('S')]
#print(key)
flag = ''
for i in range(len(c)):
    flag += chr(c[i] ^ key[i%2])
print(flag)
#HSCTF{121c8fab-bead-4a4c-852a-1522f453f135}

flag就是HSCTF{121c8fab-bead-4a4c-852a-1522f453f135}

RSA(GFSJ0820)

#RSA加密算法

RSA算法来了

先看看附件的源码加上解释

#!/usr/bin/env python3
import gmpy2
from Crypto.Util.number import getPrime
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_v1_5
from base64 import b64encode


flag = open('flag', 'r').read().strip() * 23#读取flag的内容去掉首位空白字符并重复23次


def encrypt(p, q, e, msg):
    #加密函数 encrypt
    #p，q是两个大素数
    while True:
        n = p * q#计算模数
        try:
            phi = (p - 1)*(q - 1)#计算欧拉函数 phi，用于 RSA 密钥生成。
            pubkey = RSA.construct((int(n), int(e)))#使用模数 n 和公钥指数 e 构造 RSA 公钥。
            key = PKCS1_v1_5.new(pubkey)#使用 PKCS#1 v1.5 填充方案初始化加密器。
            enc = b64encode(key.encrypt(msg))#对消息 msg 进行加密，并将加密结果编码为 Base64 字符串。
            return enc#返回加密后的 Base64 字符串，并退出函数。
        except:
            p = gmpy2.next_prime(p**2 + q**2)
            q = gmpy2.next_prime(2*p*q)
            e = gmpy2.next_prime(e**2)


p = getPrime(128)
q = getPrime(128)#生成两个 128 位的素数 p 和 q。
n = p*q#计算模数 n = p * q。
e = getPrime(64)#生成一个 64 位的素数 e 作为公钥指数。
pubkey = RSA.construct((n, e))#使用 n 和 e 构造 RSA 公钥。
with open('pubkey.pem', 'wb') as f:
    f.write(pubkey.exportKey())#生成的 RSA 公钥保存到文件 pubkey.pem 
with open('flag.enc', 'wb') as g:
    g.write(encrypt(p, q, e, flag.encode()))#encrypt 函数加密 flag，并将加密结果保存到文件 flag.enc

#pubkey
'''
-----BEGIN PUBLIC KEY-----
MEIwDQYJKoZIhvcNAQEBBQADMQAwLgIhAIk/BV0Nxf52TYgdXNYOlnshLOBJRZ5X
0uhB7UqBr3ftAgkAiLTiOfpI5Vc=
-----END PUBLIC KEY-----
'''
#flag
'''DWsGDe5mZXvs8l4kHjjteTLbV4rJ9JHwpUrZaQ/eqPT2YYiHwalRHZeobzcKRbBvcvqf1NYwJCuFwpDOnWK73bnQO06HaHdsSnRCqCy7slRnhs4QSIWkpeA3RlzSrDb/oNbuT8t/+HhlZbooWiCywnTsZWGjWwFvaGCvhEkZCLR17OB/7ZxXYhHaUCcyGmLGjpYEZGqGKU80Lu6VGenRRxmg4qsVI6T/GgXQjSZT43mIXCD+5g7zVUIfFAMQKYmwcYNWxOJZm7P9EbYQUTYNDU96hIgxrVCaMV7c1m5oLYdm99OkfyOk/lQ67KZLjSJIOSCmaJ3bHpuqDXdHPuxv9daB+31qu9eWQl2WuyuzM9U0Cd+oR+xMJcdGvLk/8wm+CPhkwnmMSVkYb7qXvaFZcap8/F5ZbzFAHLl+YKFsisRIq8iLQc1lttW7/E3dt4ds+ixfPakErgVUzKaziSDG1Ja/byqV9VdmqR0TCAtcIfmVZHu+doO1HnOJlmIb6IDwuBSwba825/E4sMM24RK/PscuXaAQGAkyKI+apX7PUObFE6XA7KMSDleikIQ7HYFsGJISGzbP0mX6iFn8qoUI82p98y2grsNBGKm3uBb3Zump8eqgJh5MMdiPCRir5uRPZpT6weepqr3i7uPTLy91QpXeG7b2OowRs6MmEB8vxyLkhIJvJrNTehXmb/2EXJwXQBEqiDAJ0+0QE0PUsegHqcYIoMNtHFt4UPX7Dm2p+Mi9a+fnXzC9GMUwqcL6JXG8W6V9yWSUBoG2mIhCX/dM2Cnrm3wprccV+Hi4gdnEfRKuDjuVBAJ0kBQrGjwK1JgoWbIItmwxGKu70olIwQN7LspUCiJH3Bkalo9crFTDGFJr7qBdMz2+7FBb7hYT9mLSxAo1UoZYtraQJoxNJQs81rG8IPq27upPj6xenTFYHhSRnJwEFAOvam2+rXTnyQO2DME='''

RSA加密算法的话可以先看看文章https://www.cnblogs.com/xiaxveliang/p/12395993.html，还是很常见的

这种算法题一般调教ai就能出来，但是得慢慢调了

解密步骤

• 从 pubkey.pem 文件中读取公钥，提取模数 n 和公钥指数 e。

  from Crypto.PublicKey import RSA
  
  with open('pubkey.pem','rb') as f:
      pubkey = RSA.importKey(f.read())
  #print(pubkey)
  
  #提取模数n和公钥指数e
  n = pubkey.n
  e = pubkey.e
  
  # print(n)
  #n = 62078208638445817213739226854534031566665495569130972218813975279479576033261
  # print(e)
  #e = 9850747023606211927

• 因为p和q只有128位，所以可以分解模数 n获取p和q，可以用大整数分解网站https://factordb.com/

所以拿到

q=184333227921154992916659782580114145999
p=336771668019607304680919844592337860739

• 计算私钥

  • 计算欧拉函数 phi = (p - 1) * (q - 1)。
  • 计算私钥指数 d = gmpy2.invert(e, phi)。

• 解密密文

  • 使用私钥和 PKCS#1 v1.5 填充方案解密 flag.enc 文件中的内容。

最终的exp

import gmpy2
from Crypto.Util.number import getPrime,inverse
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_v1_5
from base64 import b64encode, b64decode

# 读取内容
flag_encode = b64decode(open('flag.enc', 'r').read())
pubkey = RSA.importKey(open('pubkey.pem', 'r').read())

# 提取 n 和 e
n = pubkey.n  # 模数
e = pubkey.e  # 公钥指数

# print(n)
#n = 62078208638445817213739226854534031566665495569130972218813975279479576033261
# print(e)
#e = 9850747023606211927
# 分解 n 拿到 p 和 q
q = 184333227921154992916659782580114145999
p = 336771668019607304680919844592337860739

#解密
while True:
    n = p * q
    if n >= int(flag_encode.hex(), 16):
        
        #欧拉函数的phi
        phi = (p-1)*(q-1)
        #私钥模数d
        d = inverse(e,phi)
        
        #创建私钥
        privkey = RSA.construct((int(n), int(e), int(d)))
        key = PKCS1_v1_5.new(privkey)
        
        #解密
        flag = key.decrypt(flag_encode,None)
        
        #因为flag是重复了23次的
        L = len(flag) // 23
        single_flag = flag[:L]
        print(single_flag)
        break
    else:
        p = gmpy2.next_prime(p ** 2 + q ** 2)
        q = gmpy2.next_prime(2 * p * q)
        e = gmpy2.next_prime(e ** 2)

前面写的时候一直报错，PKCS#1 v1.5 要求密文的长度必须与 RSA 模数 n 的字节长度一致，一开始的模数n是解不出来的，那个仅仅是公钥里面的n，和加密函数里面的n是不一样的，所以需要爆破爆出来

线性反馈移位寄存器(GFSJ1082)

#线性反馈移位寄存器伪随机数生成器

分析一下附件

from secret import secret#从secret中导入secret
for b in secret: assert(b == '0' or b == '1')#遍历secret中的每一个字符，检查是否等于1或0
assert(len(secret) == 128)#检查secret的字符长度是否为128
# a 01 string with length 128
# your flag is flag{md5(secret).hexdigest()}#提示flag 是 secret 的 MD5 哈希值的十六进制表示

def string2bits(s):#将二进制字符串 s 转换为整数列表的函数
    return [int(b) for b in s]

def bits2string(bs):#将字符串s中的字符转化成整数
    s = [str(b) for b in bs]
    return ''.join(s)

def lfsr(state, mask):
    assert(len(state) == 128)
    assert(len(mask)  == 128)

    output = 0
    for i in range(128):
        output = output ^ (state[i] & mask[i])

    return output

if __name__ == '__main__':
    initState = [0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0]
    mask = string2bits(secret)

    for i in range(256):
        state = initState[i:]
        output = lfsr(state, mask)
        initState += [output]

    outputState = bits2string(initState[128:])
    print('outputState =', outputState)
    #
    # outputState = 1010100001001011101000000100100001101011010100101011010101011010100100001110010010110111010111110000000000011011001110100011000111110100110011011011100111000000001100001000001011010011011010110110111100110101001110001001001000001110111011110001111001111111
    #

一个基于 线性反馈移位寄存器 (LFSR) 的伪随机数生成器https://blog.csdn.net/weixin_37414365/article/details/139606928

先分析一下前面两个转化函数

def string2bits(s):#将一个二进制字符串 s 转换为一个整数列表。
    return [int(b) for b in s]

def bits2string(bs):#将一个整数列表 bs 转换回一个二进制字符串。
    s = [str(b) for b in bs]
    return ''.join(s)

不清楚的话可以直接本地测试实操一下

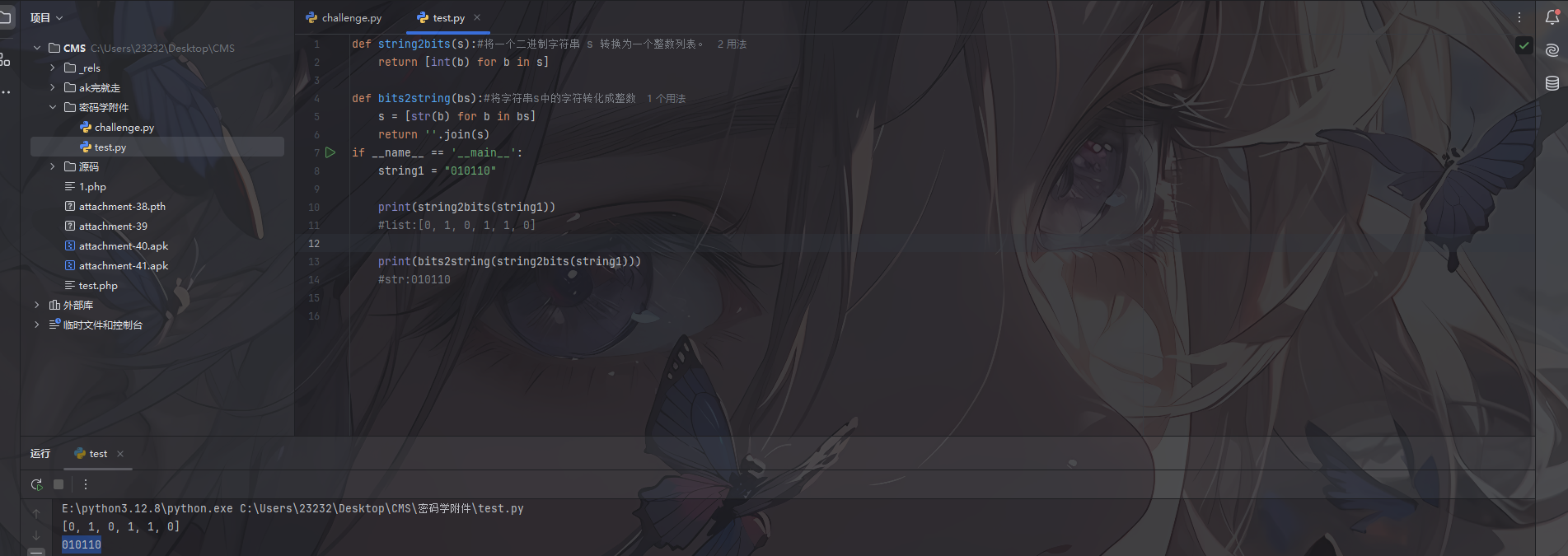
最重要的还是最后一个**线性反馈移位寄存器 (LFSR)**的实现函数

def lfsr(state, mask):
    assert(len(state) == 128)
    assert(len(mask)  == 128)

    output = 0
    for i in range(128):
        output = output ^ (state[i] & mask[i])

    return output

输入两个长度为128数组 state, mask ，输出 output 值为$out=\sum{state_i \times mask_i} \mod 2$

所以这里的话会遍历每个状态和反馈，

output = output ^ (state[i] & mask[i])

• 计算 state[i] 和 mask[i] 的按位与（&），然后与当前的 output 进行按位异或（^）。这一步实现了 LFSR 的反馈逻辑。

然后我们需要注意一个点，在二进制运算中，异或运算（^）和模 2 的加法（mod 2）是等价的，位与运算(&)和模2的乘法是等价的。

本地测试一下

那么我们就可以算进行解密了

initState是初始化数组，也是LFSR的初始状态，mask 是secret转二进制之后的内容

然后最主要的操作就是进行256轮LFSR计算，注意到每轮 state 数组取值会向右移动一个位置，同时 initState 长度会增长1，即数组尾部追加了 output 值

这里有点小复杂，看看官方wp怎么说的

关键关系式

1. 原始关系式：
   $$
   out=∑state i​×mask i​ mod2
   $$

   • 表示状态向量（state）和掩码向量（mask）的点积，再取模 2。

2. 矩阵乘法形式：
   $$
   out=State×Maskmod2
   $$

   • 这里，State 是一个 1×1281×128 的行向量，Mask 是一个 128×1128×1 的列向量。
   • 矩阵乘法的结果是一个标量（即一个数），再取模 2。

# sage
def string2bits(s):
    return [int(b) for b in s]


if __name__ == '__main__':
    initState = [0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0,
                 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0,
                 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1,
                 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0]
    outputState = string2bits(
        '1010100001001011101000000100100001101011010100101011010101011010100100001110010010110111010111110000000000011011001110100011000111110100110011011011100111000000001100001000001011010011011010110110111100110101001110001001001000001110111011110001111001111111')
    states = initState + outputState

    ms = MatrixSpace(GF(2), 128, 128)
    mv = []
    for i in range(128):
        mv += states[i: i + 128]
    m = ms(mv)

    vs = MatrixSpace(GF(2), 128, 1)
    vv = outputState[0:128]
    v = vs(vv)

    secret = m.inverse() * v
    M = secret.str().replace('\n', '').replace('[', '').replace(']', '')
    print(M)

其实这里的话也是根据一个矩阵的乘法和加法来实现二进制运算，从而进行解密

这里需要SageMath环境，可以手动安装一下，我在Ubuntu安装的

sudo apt update
sudo apt install sagemath

安装好之后直接把代码传sage里运行就行，当热也可以编辑成sage文件然后run一下

之前提示

flag{md5(secret).hexdigest()}

所以我们需要再进行解码

secret = 01000101011000010111001101111001010011010110000101110100011010000101011101101001011101000110100001010011011000010110011101100101

然后解码一下吧

import hashlib

secret_bin = "01000101011000010111001101111001010011010110000101110100011010000101011101101001011101000110100001010011011000010110011101100101"

secret_bytes = bytes([int(secret_bin[i:i+8], 2) for i in range(0, len(secret_bin), 8)])

flag = hashlib.md5(secret_bytes).hexdigest()

print(flag)

rsarsa(GFSJ1074)

#一个很简单的RSA算法

看看附件

for _ in range(3):#循环三次
    p = random_prime(2^1024)
    q = random_prime(2^1024)#两个1024位的随机素数p和q
    
    n = p*q#RSA模数n
    
    p1 = p>>724#将p右移724位，提取p的高位部分
    ct=n * inverse_mod(q % (2 ** 265), 2^265) % 2^265#计算
    print('p1=',p1)
    print('ct=',ct)
    print("n=",n)
    e = 65537#设置公钥指数e
    alarm(80)
    m = randint(2,n-1)
    c=pow(m,e,n)
    print('c=', c)
    print('---------------------------------------------')
    m1 = int(input("m="))#如果传入的m1不等于m，则报错退出
    print('---------------------------------------------')
    print()
    if m1!=m:
        print("Nope")
        exit()

print(open("flag.txt","r").read())

因为p是1024位素数，右移724位之后p1就是p的前300位

重点看ct的赋值算法

ct=n * inverse_mod(q % (2 ** 265), 2^265) % 2^265

• q % (2 ** 265)这里提取了q的最低265位二进制数，而inverse_mod(q % (2 ** 265), 2^265)是计算q的低位在模2**265下的逆元
• 将n与逆元相乘并取模2**265，确保结果的范围在 00 到 2265−12265−1 之间。

所以所以公式最终简化为
$$
ct≡pmod2 265
$$

所以结合p1和ct就可以恢复完整的p了

三次每次循环生成一个新的 RSA 密钥对，加密一个随机明文，要求用户解密。

所以我们每次都要去解出解密后的明文m1

连接一下环境

nc 223.112.5.141 60803

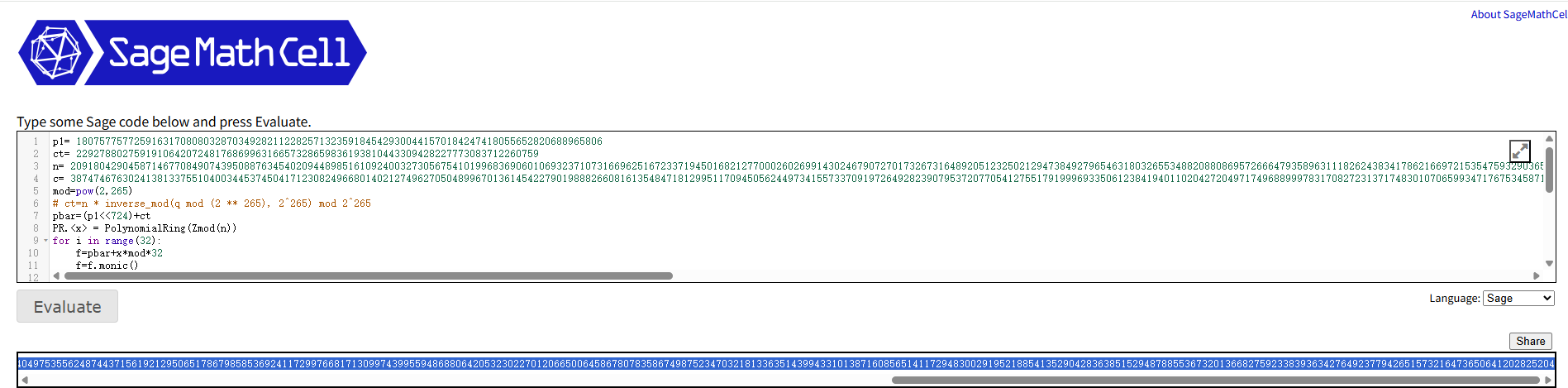
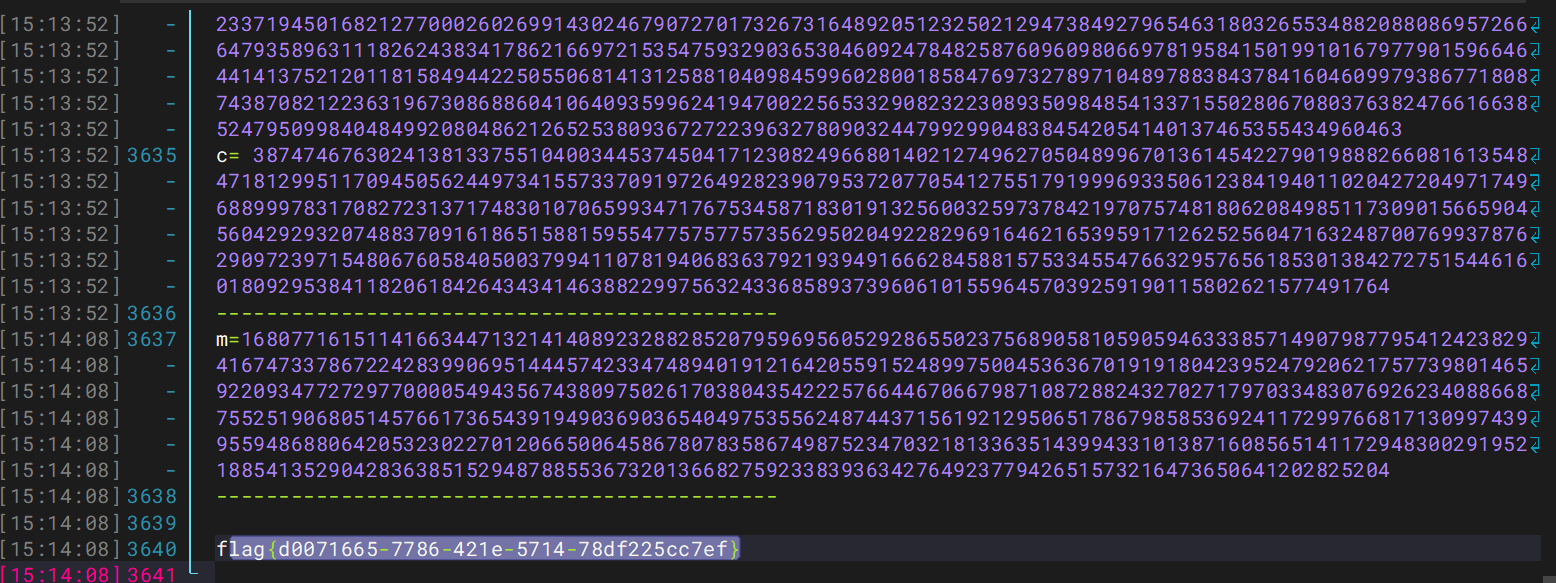
然后官方的wp解密脚本就是

p1= 1807577577259163170808032870349282112282571323591845429300441570184247418055652820688965806
ct= 22927880275919106420724817686996316657328659836193810443309428227773083712260759
n= 20918042904587146770849074395088763454020944898516109240032730567541019968369060106932371073166962516723371945016821277000260269914302467907270173267316489205123250212947384927965463180326553488208808695726664793589631118262438341786216697215354759329036530460924784825876096098066978195841501991016797790159664644141375212011815849442250550681413125881040984599602800185847697327897104897883843784160460997938677180874387082122363196730868860410640935996241947002256533290823223089350984854133715502806708037638247661663852479509984048499208048621265253809367272239632780903244799299048384542054140137465355434960463
c= 3874746763024138133755104003445374504171230824966801402127496270504899670136145422790198882660816135484718129951170945056244973415573370919726492823907953720770541275517919996933506123841940110204272049717496889997831708272313717483010706599347176753458718301913256003259737842197075748180620849851173090156659045604292932074883709161865158815955477575775735629502049228296916462165395917126252560471632487007699378762909723971548067605840500379941107819406836379219394916662845881575334554766329576561853013842727515446160180929538411820618426434341463882299756324336858937396061015596457039259190115802621577491764
mod=pow(2,265)
# ct=n * inverse_mod(q mod (2 ** 265), 2^265) mod 2^265
pbar=(p1<<724)+ct
PR.<x> = PolynomialRing(Zmod(n))
for i in range(32):
    f=pbar+x*mod*32
    f=f.monic()
    pp=f.small_roots(X=2^454,beta=0.4)
    if(pp):
        break
    pbar+=mod
assert pp
p=pbar+pp[0]*32*mod

q=n//Integer(p)
e=65537
phi=(p-1)*(q-1)
# d = gmpy2.invert(e, (p - 1) *(q - 1))
# m = powmod(c, d, n)
d = inverse_mod(e, phi)
m = pow(c, d, n)
print(m)

Untitled(GFSJ0087)

分析一下附件

from Crypto.Util.number import getPrime,long_to_bytes,bytes_to_long
import primefac
import time
from os import urandom
import hashlib
import sys
class Unbuffered(object):
   def __init__(self, stream):
       self.stream = stream
   def write(self, data):
       self.stream.write(data)
       self.stream.flush()
   def __getattr__(self, attr):
       return getattr(self.stream, attr)
import sys
sys.stdout = Unbuffered(sys.stdout)
def gen_args():
    p=getPrime(1024)
    q=getPrime(1024)
    n=p*q
    e=0x10001
    d=primefac.modinv(e,(p-1)*(q-1))%((p-1)*(q-1))
    return (p,q,e,n,d)
def proof():
    salt=urandom(4)
    print salt.encode("base64"),
    proof=raw_input("show me your work: ")
    if hashlib.md5(salt+proof.decode("base64")).hexdigest().startswith("0000"):
        print "checked success"
        return 1
    return 0

def run():
    if not proof():
        return
    m=int(open("/home/bibi/PycharmProjects/work/whctf/flag","r").read().encode("hex"),16)#flag{*}
    (p,q,e,n,d)=gen_args()
    c=pow(m,e,n)
    print "n:",hex(n)
    print "e:",hex(e)
    print "c:",hex(c)
    t=int(hex(m)[2:][0:8],16)
    u=pow(t,e,n)
    print "u:",hex(u)
    print "===="
    x=int(hex(m)[2:][0:8]+raw_input("x: "),16)
    print "===="
    y=int(raw_input("y: "),16)
    if (pow(x,e,n)==y and pow(y,d,n)==t):
        print "s:",hex(int(bin(p)[2:][0:568],2))
run()

hack_in_the_card_I(GFSJ0157)

asm(GFSJ0198)

B64(GFSJ0218)

看一下附件

#!/usr/bin/python2

from flag import flag
from base64 import b64decode
from SocketServer import ThreadingTCPServer
from sys import argv
from binascii import hexlify, unhexlify
import SocketServer
import os

N = 8
MAX_TRIES = 1024
PAD = 64

welcome = "Welcome! :-)\n"
menu = "What would you like to do:\n\t1: supply encoded input,\n\t2: tell me my secret\n> "

def gen_secret():
    return os.urandom(N)#生成 N 个字节的随机数据。

def crypt(s1, s2):
    return "".join(map(lambda c: chr(((ord(c[0])^ord(c[1]))+PAD)%256), zip(s1,s2)))
#内层将第一个和第二个字符的ASCII码值进行异或处理，然后加上常量PAD，并将结果对256取模，最后将结果转换为对应的 ASCII 字符。
#zip将 s1 和 s2 逐字符配对，生成一个元组的迭代器。
#将结果转换为字符，并连接成最终的加密字符串。

b64chars = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz+/"
def decode(s, secret):
    enc = ""#初始化一个空字符串 enc，用于存储处理后的 Base64 编码数据。
    s = crypt(s, secret)#调用 crypt 函数，对字符串 s 和 secret 进行加密操作。
    
    for c in s:#遍历s中的每个字符
        if c in b64chars:#看该字符是否符合base64规定的合法字符
            enc+=c#enc收集所有符合的合法字符

    if len(enc) % 4 == 1:#如果 enc 的长度除以 4 余 1，则去掉最后一个字符。这是因为 Base64 编码的长度必须是 4 的倍数
        enc = enc[:-1]

    while len(enc) % 4 != 0:#如果 enc 的长度不是 4 的倍数，则追加 "=" 字符，直到长度满足要求。
        enc+="="

    return b64decode(enc)
#其实就是base64的操作，只不过这里对传入的字符进行了合法的处理 

class B64Handler(SocketServer.BaseRequestHandler):
    def setup(self):
        self.tries = 0
        self.secret = gen_secret()#生成一个随机的秘密值，并将其存储在实例变量 secret 中。

    def handle(self):
        self.request.send(welcome)
        for i in range(MAX_TRIES):
            self.request.send("Round number: {}\n{}".format(i, menu))#像客户端发送当前轮次（i）和菜单选项(menu)
            if self.request.recv(2)[0] == "1":#检测客户端的输入第一个字符是否位1
                self.request.send("What would you like me to decode?\n> ")#如果选择1则返回提示信息
                answer = self.request.recv(len(self.secret))#接收用户的输入，长度为secret的长度
                decoded = decode(answer, self.secret)#进行decode函数解码操作
                self.request.send("Alright, here is your answer: {}\n".format(decoded))#输出解码后的结果

            else:
                self.request.send("Alright, what is my secret (hex encoded)?\n> ")#要求客户端输入 self.secret 的十六进制编码。
                answer = self.request.recv(2*len(self.secret)+1).rstrip()#接收客户端的输入，长度为 2*len(self.secret)+1，并去掉末尾的空白字符。
                if answer==hexlify(self.secret):#检查客户端的输入是否与 self.secret 的十六进制编码一致。
                    self.request.send("Well done, here is your flag: {}\n".format(flag))#如果一致则输出flag
                else:
                    self.request.send("This was not what I was looking for. :-(\n")
                break

        self.request.send("Bye!\n")

def main():
    SocketServer.ThreadingTCPServer.allow_reuse_address = True
    if len(argv) < 2:
        print("Usage: {} <PORT>".format(argv[0]))
    else:
        LOCAL_PORT = int(argv[1])
        s = SocketServer.ThreadingTCPServer(("", LOCAL_PORT), B64Handler)
        try:
            s.serve_forever()
        except KeyboardInterrupt:
            print("shutting down")
            s.shutdown()
            s.socket.close()

if __name__ == "__main__":
    main()

McEliece(GFSJ0219)

crackme_c1(GFSJ0281)

Luaky(GFSJ0306)

Secret_FS(GFSJ0307)

broken-box(GFSJ0432)

neo(GFSJ0433)

fez(GFSJ0783)